Содержание
Связи и реакции связей
Все тела делятся на свободные и связанные.
Свободные тела – это тела, перемещение которых не ограничено.
Связанные тела – это тела, перемещение которых ограничено другими телами.
Тела, ограничивающие перемещение других тел, называют связями.
Силы, действующие от связей и препятствующие перемещению, называют реакциями связей. Реакция связи всегда направлена с той стороны, куда нельзя перемещаться.
Всякое связанное тело можно представить свободным, если связи заменить их реакциями (принцип освобождения от связей).
Связи делятся на несколько типов.
Связь – гладкая опора (без трения) – реакция опоры приложена в точке опоры и всегда направлена перпендикулярно опоре.
Гибкая связь (нить, веревка, трос, цепь) – груз подвешен на двух нитях. Реакция нити направлена вдоль нити от тела, при этом нить может быть только растянута.
Жесткий стержень – стержень может быть сжат или растянут. Реакция стержня направлена вдоль стержня. Стержень работает на растяжение или сжатие. Точное направление реакции определяют, мысленно убрав стержень и рассмотрев возможные перемещения тела без этой связи.
Возможным перемещением точки называется такое бесконечно малое мысленное перемещение, которое допускается в данный момент.
Шарнирная опора. Шарнир допускает поворот вокруг точки закрепления. Различают два вида шарниров.
Подвижный шарнир. Стержень, закрепленный на шарнире, может поворачиваться вокруг шарнира, а точка крепления может перемещаться вдоль направляющей (площадки). Реакция подвижного шарнира направлена перпендикулярно опорной поверхности, так как не допускается только перемещение поперек опорной поверхности.
Неподвижный шарнир. Точка крепления перемещаться не может.
Стержень может свободно поворачиваться вокруг оси шарнира. Реакция такой опоры проходит через ось шарнира, но неизвестна по направлению. Ее изображают в виде двух составляющих: горизонтальной и вертикальной (Rx, Ry).
Защемление, или «заделка». Любые перемещения точки крепления невозможны.
Под действием внешних сил в опоре возникают реактивная сила и реактивный момент Мz, препятствующий повороту.
Реактивная сила представляется в виде двух составляющих вдоль осей координат:
R = Rx+ Ry.
Частные случаи приведения
1.R=0,M≠0 –
система эквивалентна паре
сил с моментом, равным
главному моменту системы, который в
этом случае не зависит от выбора центра
приведения;
2.
R≠0,M=0 –
система эквивалентна равнодействующей R.Главный вектор в
данном случае – является равнодействующей.
3.
R≠0,M≠0 –
система эквивалентна равнодействующей R,приложенной в новом
центре приведения, расположенном от
прежнего на расстоянии d
= Мо\R
4.
R=0,M=0 –
плоская система сил находится в
равновесии;
Теорема
Вариньона (о моменте равнодействующей
плоской системы сил)
Момент
равнодействующей плоской системы сил
относительно произвольного центра О
равен алгебраической сумме моментов
всех сил системы относительно этого
центра.
Аналитические
уравнения равновесия плоской системы
сил
-
Условие равновесия выражается тремя
уравнениями – основные уравнения
равновесия:
2. Варианты записи уравнений равновесия
– в зависимости от расположения сил
или
Класссификация нагрузок
-
Сосредоточенная
-
Распределённая: по линии, по поверхности,
по объёму -
Изгибающий момент
Балочные системы
1. Объект решения задач статики – балки
(или балочные системы)
2. Балка – деталь в виде прямого бруса
с опорами в двух (или более) точках.
Виды
опор
1.
Шарнирно-подвижная: вращение вокруг
своей оси (шарнир) + поступательное
перемещение (подвижная)
2.
Шарнирно-неподвижная: вращение вокруг
своей оси (шарнир)
3. Жёсткая
заделка(защемление): препятствует
любому перемещению.
Решение
задач на определение опорных реакций
С
помощью трёх уравнений равновесия
определяют реакции опор (если число
реакций связи не превышает трёх):
1.
Показать нагрузки
2.
Обозначают нагрузки
3.
Освобождаются от опор и заменяют их
действие на балку реакциями
4.
Составляют уравнение равновесия
5.
Решают уравнения равновесия и определяют
из них опорные реакции
6.
Проверка решения
Определение
усилий в стержнях плоских ферм –
вырезанием узлов
1. Аналитический
способ
2. Графический
способ – построением диаграммы Максвелла
– Кремоны
Элементы
теории трения
ТЕМА
1.5. ЭЛЕМЕНТЫ ТЕОРИИ ТРЕНИЯ
(авто — 1 час)
Самостоятельная
работа обучающегося (авто
– 1час)
1.
Решение задач по индивидуальным заданиям
1. Понятие
о трении
Сила трения
возникает при соприкосновении тел и
препятствует передвижению одного тела
по поверхности другого.
2. Виды сил
трения:
А) трение
скольжения
Б) трение
скольжения
3. Трение
скольжения– сопротивление, возникающее
при относительном перемещении одного
тела по поверхности другого.
4. Законы
трения:
А) Сила трения
Fтрнаправлена в
сторону, противоположную относительной
скорости скольжения
Б) Сила трения
не зависит от площади контактирующих
поверхностей
В) Модуль
силы трения пропорционален нормальному
давлению (чем больше нормальное давление,
тем больше сила трения).
5. По рисунку:
А) сила тяжести
mg– вниз (чем большеmg,
тем больше опорная реакцияN(вектор)
Б) тело
движется вниз = сила трения направлена
вверх по наклонной плоскости
В) гладкая
поверхность = опорная реакция N(вектор) направлена перпендикулярна
плоскости
Г) по аксиоме
3 строим диагональ параллелограмма R(равнодействующая)
6. Виды сил
трения скольжения:
А) сила трения
при покое FтрfoN
Б) сила трения
при движении FтрfN
N– сила нормального давления
fo– коэффициент трения покоя
f– коэффициент трения скольжения –
зависит от скорости скольжения тел.
Оба коэффициента
зависят от материала и физического
состояния поверхностей
7. Трение
качения– сопротивление, возникающее
при качении одного тела к другому.
8. Виды
связей:
А) идеальные
(без трения)
Б) реальные
(с трением)
Самостоятельная
работа обучающихся – 3час эзс, 4час арх,
1.
Решить задачи по определению опорных
реакций для однопролётной балки по
вариантам
2.
Решить задачи на определение усилий в
стержнях фермы по вариантам
3.
Сравнить способы определения усилий,
сделать краткий анализ о преимуществах
и недостатках каждого метода — результат
оформить в виде таблицы
Авто
– 2час
1.
Выполнение расчётно-графической
работы на определение опорных реакций
балочных систем
ГДЗ Физика 7 класс. Перышкин отдыхает! Рычаг. Блок. Момент силы
- Подробности
- Просмотров: 140
Назад в «Оглавление»
Давненько пользуемся мы этими учебниками.
Еще наши мамы и папы по ним учились.
Как же осилить домашнее задание, ответить на вопросы и решить задачи в упражнениях?
Уверена, что думающие ученики сначала всё сделают сами, а эти сведения будут помощью «застрявшим в пути».
Ответы на ДЗ по физике помогут вам проверить себя и найти ошибки.
Ответы на ДЗ из упражнений соответствуют всем выпускам учебников этого автора, начиная с 1989 г.
Так как номера упражнений с одинаковыми вопросами в разных выпусках различаются, ответы на вопросы к упражнениям скомпонованы по темам.
На этой странице представлены решения задач по параграфам: Простые механизмы. Рычаг. Равновесие сил на рычаге. Момент силы. Рычаги в технике, быту и природе.
Заодно некоторые узнают, какую тему по физике они сейчас изучают))
Так нет ли здесь нужной вам задачи?
Обязательно найдется!
Решаем вместе?
1. Укажите точку опоры и плечи сил у рычагов, изображенных на рисунках.
а) Тачка с одним колесом.
Схема рычага:
Точка опоры — ось колеса (О).
Плечо силы F1 — от оси колеса до груза на тачке (ОА).
Плечо силы F2 — от оси колеса до рук (ОВ).
б) Рука человека — это тоже рычаг.
Схема рычага:
Точка опоры — локтевой сустав (О).
Плечо силы F1 — длина руки (предплечья) от локтя до кисти, в которую вложен груз (ОА).
Плечо силы F2 — небольшое расстояние (около 3 см) от локтевого сустава до точки прикрепления мышцы плеча на предплечье (ОВ).
в) Ножной тормоз в автомобиле.
Схема рычага:
Рычаг — педаль тормоза.
Точка опоры — ось вращения педали (О).
Плечо силы F1 — кратчайшее расстояние (ОА) от точки опоры до линии приложения силы F1, с которой нога давит на педаль.
Плечо силы F2 — кратчайшее расстояние (ОВ) от точки опоры до линии приложения силы F2 — силы упругости троса, прикрепленного к педали.
д, г) Палка для переноса тяжестей.
Схема рычага:
Здесь точка опоры — плечо человека (О).
Плечо силы F2 — от плеча до места, за которое держат палку (ОВ).
Плечо силы F1 — от плеча до того места, где подвешен груз (ОА).
2. Рассмотрите рисунки переноса груза на палке. При каком расположении груза на палке момент его силы тяжести больше? В каком случае груз легче нести? Почему?
Момент силы тяжести груза больше, когда увеличивается плечо этой силы.
Чтобы легче было нести, надо уменьшить плечо этой силы, т.е.расстояние от плеча до груза.
В этом случае рычаг можно уравновесить меньшей силой рук.3. Пользуясь рисунком гребца в лодке, объясните, почему при гребле мы получаем проигрыш в силе и для чего это нужно.
Весло при гребле на лодке представляет собой рычаг.
Точка опоры — уключина.
С одной стороны к рукоятке весла прикладывается сила человека.
Плечо этой силы небольшая часть весла от уключины до руки.
С другой стороны действующая на весло сила — это сила сопротивления воды.
Плечо этой силы — наиболее длинная часть весла от уключины до конца весла в воде.
Чтобы сделать гребок надо уравновесить этот рычаг,
По правилу равновесия рычага при этом к короткой части весла прикладывается большая сила, а к длинной части весла меньшая сила.
В данном случае наблюдается проигрыш в силе.
Однако при гребке расстояние, которое проходит конец весла много больше расстояния, которое проходит рукоять весла.
Проигрывая в силе, выигрываем в расстоянии, что и является целью передвижения на лодке.
Иногда когда человеку становится трудно грести (он устал), он сдвигает весло в уключине так, чтобы часть весла от руки до уключины стала длиннее. Концы весел в лодке как бы нахлестывают друг на друга, грести становится не очень удобно, зато легче, прикладывается меньшая сила. Но одновременно и расстояние, которое проходит лодка за гребок уменьшается.4. На рисунке 162 изображен разрез предохранительного клапана. Рассчитайте, какой груз надо повесить на рычаг, чтобы пар через клапан не выходил. Давление в котле в 12 раз больше нормального атмосферного давления. Площадь клапана S = 3 см2, вес клапана и вес рычага не учитывать. Плечи сил измерьте по рисунку. Куда нужно переместить груз, если давление пара в котле увеличится? уменьшится? 
Назад в «Оглавление»
Бизнес и финансы
БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством
Доказательство свойств
Перемещение точки приложения силы вдоль линии ее действия
Если точку приложения силы переместить вдоль линии действия силы, то момент, при таком перемещении, не изменится.
Доказательство
Пусть сила приложена в точке . Через точку проведем прямую, параллельную вектору силы. Эта прямая является линией ее действия. Переместим точку приложения силы в точку , принадлежащую линии действия. Тогда. Вектор проведен через две точки линии действия. Поэтому его направление совпадает или противоположно направлению вектора силы . Тогда , где – параметр; . , если точка смещена относительно в направлении вектора . В противном случае .
Таким образом, вектор, проведенный из в , имеет вид:. Найдем момент силы, приложенной в точке , применяя свойства векторного произведения:. Мы видим, что момент не изменился:.
Свойство доказано.
Абсолютная величина момента силы
Абсолютная величина момента силы относительно некоторой точки равна произведению абсолютного значения силы на плечо этой силы относительно выбранной точки.
Доказательство
Абсолютное значение момента M относительно точки O равно произведению силы F на ее плечо d = |OD|.
Пусть мы имеем силу , приложенную в точке . Рассмотрим момент этой силы относительно некоторой точки . Заметим, что точки , и вектор лежат в одной плоскости. Изобразим ее на рисунке. Через точку , в направлении вектора проводим прямую . Эта прямая называется линией действия силы . Через точку опустим перпендикуляр к линии действия. И пусть является точкой пересечения линии действия и перпендикуляра. Тогда – плечо силы относительно центра . Обозначим его буквой . Воспользуемся , согласно которому точку приложения силы можно перемещать вдоль ее линии действия. Переместим ее в точку . Момент силы:. Поскольку векторы и перпендикулярны, то по свойству векторного произведения, абсолютное значение момента:, где – абсолютное значение силы.
Заметим, что вектор момента перпендикулярен плоскости рисунка. Его направление определяется по правилу правого винта. Если мы будем вращать винт, проходящий через точку перпендикулярно плоскости рисунка, в направлении силы , то он будет перемещаться на нас. Поэтому вектор момента перпендикулярен плоскости рисунка и направлен на нас.
Свойство доказано.
Момент относительно точки от силы, проходящей через эту точку
Момент относительно точки , от силы, линия действия которой проходит через эту точку, равен нулю.
Доказательство
Пусть линия действия силы проходит через точку . Тогда плечо этой силы относительно равно нулю: . Согласно , абсолютное значение момента силы относительно выбранной точки равно нулю:.
Свойство доказано.
Момент суммы сил, приложенных в одной точке
Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:.
Доказательство
Пусть силы приложены в одной точке . Пусть – векторная сумма этих сил. Находим момент относительно некоторой точки от векторной суммы , приложенной в точке . Для этого применяем свойства векторного произведения:.
Свойство доказано.
Момент системы сил, векторная сумма которых равна нулю
Если векторная сумма сил равна нулю:, то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:.
Доказательство
Пусть силы приложены в точках , соответственно. И пусть точки и обозначают два центра, относительно которых мы будем вычислять моменты. Тогда имеют место следующие векторные уравнения:. Используем их при вычислении суммы моментов относительно точки . Здесь мы воспользовались тем, что по условию,.
Свойство доказано.
Момент относительно оси от силы, проходящей через эту ось
Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство
В указано, что момент силы относительно оси – это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси. В качестве такой точки возьмем точку пересечения линии действия силы с осью. Но, согласно , момент относительно этой точки равен нулю. Поэтому равна нулю и его проекция на эту ось.
Свойство доказано.
Момент относительно оси от силы, параллельной этой оси
Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство
Пусть – произвольная точка на оси. Рассмотрим момент силы относительно этой точки. Согласно определению:. Согласно свойству векторного произведения, вектор момента перпендикулярен вектору силы . Поскольку вектор силы параллелен оси, то вектор момента ей перпендикулярен. Поэтому проекция момента относительно точки на ось равна нулю.
Свойство доказано.
Определение равнодействующей геометрическим способом
Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;…; Fn), где n – число сил, входящих в систему.
В соответствии со следствиями из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными к одной точке.
Используя свойство векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил.
При графическом способе определения равнодействующей векторы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится.
Вектор равнодействующей направлен навстречу векторам сил-слагаемых. Такой способ получения равнодействующей называется геометрическим.
Многоугольник сил строится в следующем порядке.
1. Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпал с началом последующего.
2. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу.
3. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.
Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого.
Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут.
Если в системе три силы, образуется треугольник сил.
Геометрическим способом пользуются, если в системе три силы. При решении задач на равновесие тело считается абсолютно твердым (отвердевшим).
Задачи решаются в следующем порядке.
1. Определить возможное направление реакций связей.
2. Вычертить многоугольник сил системы, начиная с известных сил, в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура).
3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.
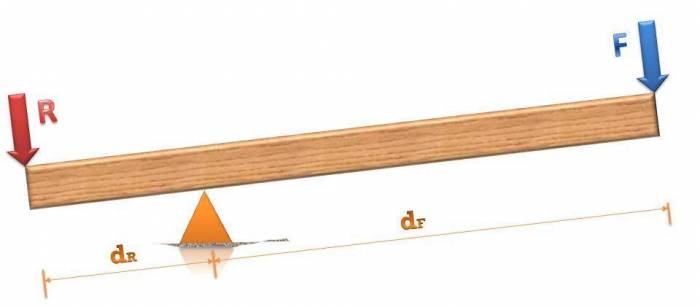
Что такое рычаг силы?
Рычаг силы играет важную роль при определении величины момента силы. Чтобы понять, о чем идет речь, рассмотрим следующий рисунок.
Здесь показан некоторый стержень длиною L, который закреплен в точке вращения одним из своих концов. На другой конец действует сила F, направленная под острым углом φ. Согласно определению момента силы, можно записать:
Угол (180o-φ) появился потому, что вектор L¯ направлен от закрепленного конца к свободному. Учитывая периодичность тригонометрической функции синуса, можно переписать это равенство в таком виде:
Теперь обратим внимание на прямоугольный треугольник, построенный на сторонах L, d и F. По определению функции синуса, произведение гипотенузы L на синус угла φ дает значение катета d
Тогда приходим к равенству:
Линейная величина d называется рычагом силы. Он равен расстоянию от вектора силы F¯ до оси вращения. Как видно из формулы, понятием рычага силы удобно пользоваться при вычислении момента M. Полученная формула говорит о том, что вращающий момент максимальный для некоторой силы F будет возникать только тогда, когда длина радиус-вектора r¯ (L¯ на рисунке выше) будет равна рычагу силы, то есть r¯ и F¯ будут взаимно перпендикулярны.
Смещение и вращение из-за силы
Точечные силы
Когда на частицу действует сила, она применяется к одной точке (объем частицы незначителен): это точечная сила, и частица является точкой ее приложения. Но внешняя сила, действующая на протяженное тело (объект), может быть приложена к ряду составляющих его частиц, т.е. может «распространяться» по некоторому объему или поверхности тела. Однако определение его вращательного воздействия на тело требует, чтобы мы указали его точку приложения (фактически, линию приложения, как объяснено ниже). Проблема обычно решается следующими способами:
- Часто объем или поверхность, на которую действует сила, относительно малы по сравнению с размером тела, так что их можно аппроксимировать точкой. Обычно нетрудно определить, является ли ошибка, вызванная таким приближением, допустимой.
- Если это неприемлемо (очевидно, например, в случае силы тяжести), такую силу «объем / поверхность» следует описать как систему сил (компонентов), каждая из которых действует на отдельную частицу, и затем расчет должен быть выполнен для каждый из них отдельно. Такой расчет обычно упрощается за счет использования дифференциальных элементов объема / поверхности тела и интегрального исчисления. Однако в ряде случаев можно показать, что такая система сил может быть заменена одноточечной силой без фактического расчета (как в случае однородной гравитационной силы).
В любом случае анализ движения твердого тела начинается с модели точечной силы. И когда сила, действующая на тело, отображается графически, ориентированный линейный сегмент, представляющий силу, обычно рисуется так, чтобы «начать» (или «закончить») в точке приложения.
Твердые тела
Как сила ускоряет тело.
В примере, показанном на диаграмме напротив, единственная сила действует в точке приложения H на свободное твердое тело. Тело имеет массу , и его центр масс является точкой С . В приближении постоянной массы сила вызывает изменения в движении тела, описываемые следующими выражениями:
F→{\ displaystyle \ scriptstyle {\ vec {F}}}м{\ displaystyle \ scriptstyle m}
- а→знак равноF→м{\ displaystyle {\ vec {a}} = {{\ vec {F}} \ over m}} центр ускорения масс; и
- α→знак равноτ→я{\ displaystyle {\ vec {\ alpha}} = {{\ vec {\ tau}} \ над I}} — угловое ускорение тела.
Во втором выражении — крутящий момент или момент силы, тогда как — момент инерции тела. Крутящий момент, вызванный силой, — это векторная величина, определенная относительно некоторой контрольной точки:
τ→{\ displaystyle \ scriptstyle {\ vec {\ tau}}}я{\ displaystyle \ scriptstyle I}F→{\ displaystyle \ scriptstyle {\ vec {F}}}
- τ→знак равнор→×F→{\ displaystyle {\ vec {\ tau}} = {\ vec {r}} \ times {\ vec {F}}} — вектор крутящего момента, а
- τзнак равноFk{\ Displaystyle \ \ тау = Fk} количество крутящего момента.
Вектор представляет собой вектор положения точки приложения силы, и в этом примере он обращается от центра масс в качестве опорной точки (см диаграмму). Отрезок прямой — это плечо рычага силы по отношению к центру масс. Как показано на рисунке, крутящий момент не изменяется (то же плечо рычага), если точка приложения перемещается вдоль линии приложения силы (пунктирная черная линия). Более формально это следует из свойств векторного произведения и показывает, что вращательное действие силы зависит только от положения линии ее приложения, а не от конкретного выбора точки приложения вдоль этой линии.
р→{\ displaystyle \ scriptstyle {\ vec {r}}}k{\ displaystyle \ scriptstyle k}F→{\ displaystyle \ scriptstyle {\ vec {F}}}
Вектор крутящего момента перпендикулярен плоскости, определяемой силой и вектором , и в этом примере он направлен к наблюдателю; вектор углового ускорения имеет то же направление. Правилу правой руки относится это направление к по часовой стрелке или против часовой стрелки , вращение в плоскости чертежа.
р→{\ displaystyle \ scriptstyle {\ vec {r}}}
Момент инерции рассчитывается относительно оси, проходящей через центр масс, параллельной крутящему моменту. Если тело, показанное на рисунке, представляет собой однородный диск, этот момент инерции равен . Если диск имеет массу 0,5 кг и радиус 0,8 м, момент инерции составляет 0,16 кгм 2 . Если сила составляет 2 Н, а плечо рычага 0,6 м, величина крутящего момента составляет 1,2 Нм. В показанный момент сила дает диску угловое ускорение α = τ / I = 7,5 рад / с 2 , а его центру масс — линейное ускорение a = F / m = 4 м / с 2. .
я{\ displaystyle \ scriptstyle I}язнак равномр22{\ displaystyle \ scriptstyle I = мистер ^ {2} / 2}
Справочная информация
ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной
 Момент силы
Момент силы Метод определения силы мышц кисти называется кистевая динамометрия
Метод определения силы мышц кисти называется кистевая динамометрия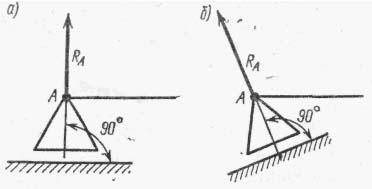 Техническая механика
Техническая механика




 Как работать с точкой здоровья юн цюань
Как работать с точкой здоровья юн цюань Точки на спине для массажа: подробное описание
Точки на спине для массажа: подробное описание Читаем холм аполлона: талантливый обладатель с энергией солнца
Читаем холм аполлона: талантливый обладатель с энергией солнца Что такое кредитное плечо?
Что такое кредитное плечо?