Содержание
20.Проекция силы на ось и на плоскость
Скалярная
величина, равная взятой с соответствующим
знаком длине отрезка, заключенного
между проекциями начала и конца силы
называется проекцией силы на ось.
Знак
плюс проекция имеет, если перемещение
от начала к концу происходит в положительном
направлении оси, и знак минус если в
отрицательном.
Таким
образом, проекции данной силы на любые
параллельные и одинаково направленные
оси равны друг другу.
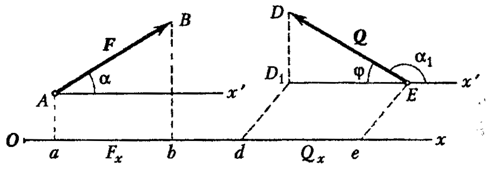
Проекция
силы
на
ось Ох обозначается какTo
есть проекция силы на ось равна
произведению модуля силы на косинус
угла между направлением силы и
положительным направлением оси.
Если
сила перпендикулярна оси, то ее проекция
на эту ось равна нулю.
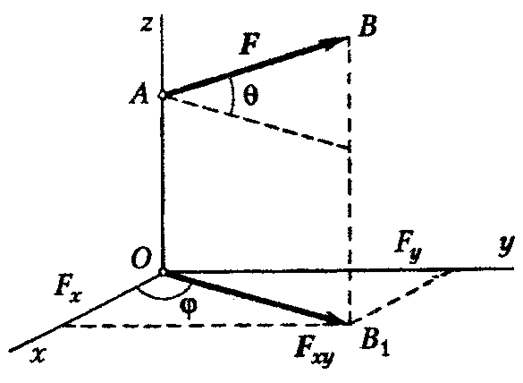
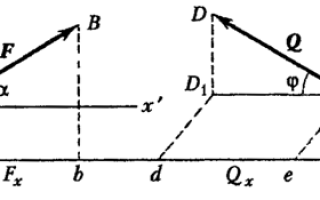
Проекцией
силы
на
плоскость Оху называется вектор,
заключенный между проекциями начала и
конца силы F на эту плоскость (рис. 13).
Проекция
силы на плоскость есть величина векторная
и характеризуется как модулем, так и
направлением в плоскости Оху. Модуль
проекции силы
на
плоскость Оху выражается какТогда проекции на оси Ох и Оу:
21.
разложение сил.
Разложить данную силу на несколько
составляющих —
значит
найти такую систему нескольких сил, для
которой данная сила является
равнодействующей. Эта задача является
неопределенной и имеет однозначное
решение лишь при задании дополнительных
условий. Рассмотрим два частных случая:
а) разложение
силы по двум заданным направлениям.
Задача сводится к построению такого
параллелограмма, у которого разлагаемая
сила является диагональю, а стороны
параллельны заданным направлениям
б)разложение
силы по трем заданным направлениям.
Если заданные направления не лежат в
одной плоскости, то задача»является
определенной и сводится к построению
такого параллелепипеда, у которого
диагональ изображает заданную
силу R,
а ребра параллельны заданным направлениям.
Способом разложения можно в простейших
случаях пользоваться для определения
сил давления на связи. Для
этого
действующую на тело (конструкцию)
заданную силу надо разложить по
направлениям реакции связей, так как
согласно закону о действии и противодействии
сила давления на связь и реакция связи
направлены вдоль одной и той же прямой.
Справочная информация
ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной
Частные случаи приведения
1.R=0,M≠0 –
система эквивалентна паре
сил с моментом, равным
главному моменту системы, который в
этом случае не зависит от выбора центра
приведения;
2.
R≠0,M=0 –
система эквивалентна равнодействующей R.Главный вектор в
данном случае – является равнодействующей.
3.
R≠0,M≠0 –
система эквивалентна равнодействующей R,приложенной в новом
центре приведения, расположенном от
прежнего на расстоянии d
= Мо\R
4.
R=0,M=0 –
плоская система сил находится в
равновесии;
Теорема
Вариньона (о моменте равнодействующей
плоской системы сил)
Момент
равнодействующей плоской системы сил
относительно произвольного центра О
равен алгебраической сумме моментов
всех сил системы относительно этого
центра.
Аналитические
уравнения равновесия плоской системы
сил
-
Условие равновесия выражается тремя
уравнениями – основные уравнения
равновесия:
2. Варианты записи уравнений равновесия
– в зависимости от расположения сил
или
Класссификация нагрузок
-
Сосредоточенная
-
Распределённая: по линии, по поверхности,
по объёму -
Изгибающий момент
Балочные системы
1. Объект решения задач статики – балки
(или балочные системы)
2. Балка – деталь в виде прямого бруса
с опорами в двух (или более) точках.
Виды
опор
1.
Шарнирно-подвижная: вращение вокруг
своей оси (шарнир) + поступательное
перемещение (подвижная)
2.
Шарнирно-неподвижная: вращение вокруг
своей оси (шарнир)
3. Жёсткая
заделка(защемление): препятствует
любому перемещению.
Решение
задач на определение опорных реакций
С
помощью трёх уравнений равновесия
определяют реакции опор (если число
реакций связи не превышает трёх):
1.
Показать нагрузки
2.
Обозначают нагрузки
3.
Освобождаются от опор и заменяют их
действие на балку реакциями
4.
Составляют уравнение равновесия
5.
Решают уравнения равновесия и определяют
из них опорные реакции
6.
Проверка решения
Определение
усилий в стержнях плоских ферм –
вырезанием узлов
1. Аналитический
способ
2. Графический
способ – построением диаграммы Максвелла
– Кремоны
Элементы
теории трения
ТЕМА
1.5. ЭЛЕМЕНТЫ ТЕОРИИ ТРЕНИЯ
(авто — 1 час)
Самостоятельная
работа обучающегося (авто
– 1час)
1.
Решение задач по индивидуальным заданиям
1. Понятие
о трении
Сила трения
возникает при соприкосновении тел и
препятствует передвижению одного тела
по поверхности другого.
2. Виды сил
трения:
А) трение
скольжения
Б) трение
скольжения
3. Трение
скольжения– сопротивление, возникающее
при относительном перемещении одного
тела по поверхности другого.
4. Законы
трения:
А) Сила трения
Fтрнаправлена в
сторону, противоположную относительной
скорости скольжения
Б) Сила трения
не зависит от площади контактирующих
поверхностей
В) Модуль
силы трения пропорционален нормальному
давлению (чем больше нормальное давление,
тем больше сила трения).
5. По рисунку:
А) сила тяжести
mg– вниз (чем большеmg,
тем больше опорная реакцияN(вектор)
Б) тело
движется вниз = сила трения направлена
вверх по наклонной плоскости
В) гладкая
поверхность = опорная реакция N(вектор) направлена перпендикулярна
плоскости
Г) по аксиоме
3 строим диагональ параллелограмма R(равнодействующая)
6. Виды сил
трения скольжения:
А) сила трения
при покое FтрfoN
Б) сила трения
при движении FтрfN
N– сила нормального давления
fo– коэффициент трения покоя
f– коэффициент трения скольжения –
зависит от скорости скольжения тел.
Оба коэффициента
зависят от материала и физического
состояния поверхностей
7. Трение
качения– сопротивление, возникающее
при качении одного тела к другому.
8. Виды
связей:
А) идеальные
(без трения)
Б) реальные
(с трением)
Самостоятельная
работа обучающихся – 3час эзс, 4час арх,
1.
Решить задачи по определению опорных
реакций для однопролётной балки по
вариантам
2.
Решить задачи на определение усилий в
стержнях фермы по вариантам
3.
Сравнить способы определения усилий,
сделать краткий анализ о преимуществах
и недостатках каждого метода — результат
оформить в виде таблицы
Авто
– 2час
1.
Выполнение расчётно-графической
работы на определение опорных реакций
балочных систем
Бизнес и финансы
БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством
3.1. Пара сил. Эквивалентность пар сил
Система
двух параллельных сил, равных по модулю
и направленных в противоположные
стороны, называется парой
сил
или просто парой
(рис. 3.1). Понятие о паре сил ввел в
механику французский ученый Луи Пуансон
(1777–1859).
Рис. 3.1. Пара
сил
Пара
сил – неуравновешенная система и не
имеет равнодействующей. Пара сил
производит на тело вращательное действие.
Вращательный
эффект пары измеряется взятым со знаком
«плюс» или «минус» произведением модуля
одной из сил пары на ее плечо (момент
пары):
 .
.
Знак
«плюс»
ставится перед числовым значением
момента в том случае, если пара стремится
повернуть тело против хода часовой
стрелки, и знак
«минус»–
если
пара стремится повернуть тело по ходу
часовой стрелки (рис. 3.2).
Рис. 3.2. Правило
знаков момента пары сил
В
Международной системе единиц (СИ) моменты
пар выражаются в
или .
.
Вращательное
действие расположенной в данной плоскости
пары зависит только от ее момента,
поэтому для задания пары сил достаточно
указать числовое значение ее момента,
а затем по данному или выбранному
плечу определить силы пары или по силам
подобрать необходимое плечо. Исходя из
этого, на рисунках и схемах пары сил
изображают иногда просто круговой
стрелкой, характеризующей лишь
направление вращающего действия.
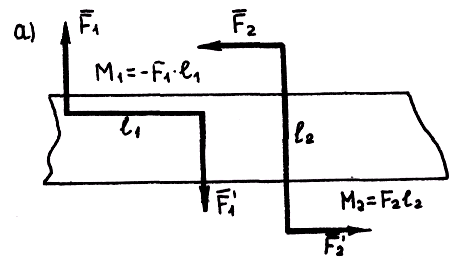
Например, пары (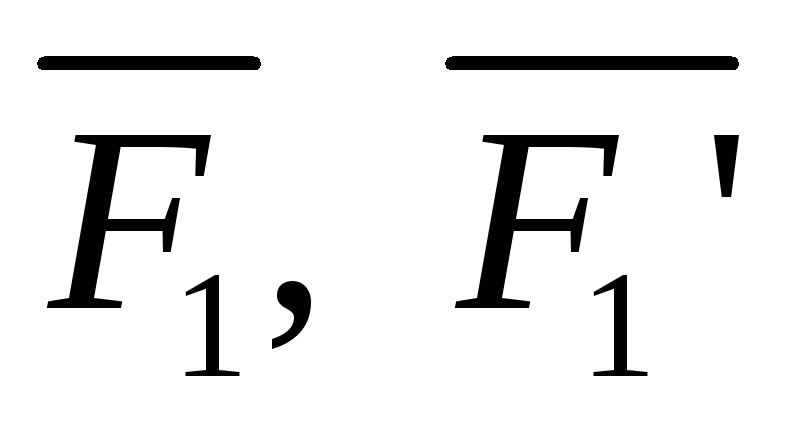
и ( )
)
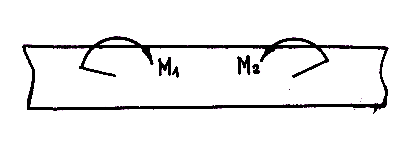
(рис. 3.3, а),
приложенные к брусу, можно условно
изобразить круговыми стрелками, обозначив
их M1
и M2
(рис. 3.3, б).
а
б
Рис. 3.3. Изображение
пары сил
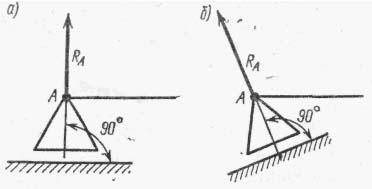
Опорные устройства балочных систем
Применяются
следующие виды опор:
Шарнирно
— подвижная опора
Здесь
остается неизвестным числовое значение
опорной реакции RA.
Следует отметить, что опорная
поверхность шарнирно-подвижной опоры
может быть непараллельна оси балки
(рис.б). Реакция RA
в этом случае не будет перпендикулярна
оси балки, так как она перпендикулярна
опорной поверхности.
Шарнирно
— неподвижная опора
Эта
опора допускает поворот вокруг оси
шарнира, но не допускает никаких линейных
перемещений. В данном случае известна
только точка приложения опорной реакции
— центр шарнира; направлениеи значение
опорной реакции неизвестны. Обычно
вместо определения значения и направления
(полной)реакции RA
находят ее составляющие RAx
и RAy.
Жесткая
заделка (защемление)Такая опора не
допускает ни линейных перемещений, ни
поворота.Неизвестными в данном случае
являются не только значение и направление
реакции, но и точка ее приложения. Поэтому
жесткую заделку заменяют силой реакции
RA
и парой сил с моментом MA.
Для
определения опорной реакции следует
найти три неизвестных: составляющие
RAx
и RAy
опорной реакции по осям координат и
реактивный момент MA.
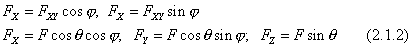
 Плечом силы называется
Плечом силы называется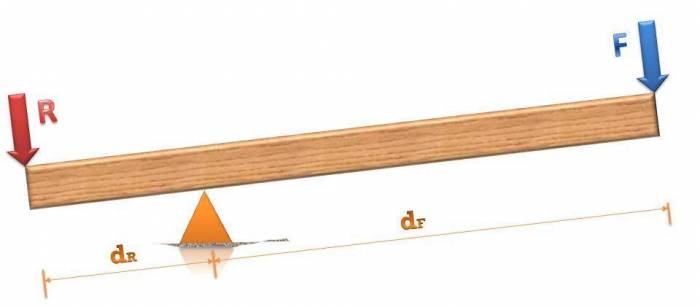 Момент силы
Момент силы Кисти coreldraw
Кисти coreldraw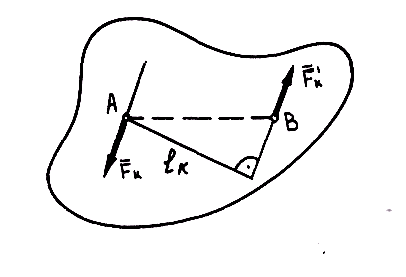

 Как утюжить припуски
Как утюжить припуски Метод определения силы мышц кисти называется кистевая динамометрия
Метод определения силы мышц кисти называется кистевая динамометрия Связки коленного сустава: анатомия
Связки коленного сустава: анатомия Освобождение от захватов: основные методы, типовые приемы самозащиты
Освобождение от захватов: основные методы, типовые приемы самозащиты