Содержание
- 1 Справочная информация
- 2 ТИПЫ И ОСНОВНЫЕ РАЗМЕРЫ
- 3 Доказательство свойств
- 4 Как снять квартиру без залога?
- 5 Бизнес и финансы
- 6 ГДЗ Физика 7 класс. Перышкин отдыхает! Рычаг. Блок. Момент силы
- 7 Кредитное плечо: чем оно выгодно трейдеру
- 8 Лабораторная работа №7 Сила мышц и силовая выносливость
- 9 Используем векторы для изучения вращательного движения
- 10 Что такое рычаг силы?
- 11 Как принцип рычага реализован в нашем теле
- 12 Сила трения
- 13 Заблуждения о кредитном плече
- 14 Переходим от прямолинейного движения к вращательному
- 15 Равновесие рычага
Справочная информация
ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной
ТИПЫ И ОСНОВНЫЕ РАЗМЕРЫ
1. ТИПЫ И ОСНОВНЫЕ РАЗМЕРЫ
Доказательство свойств
Перемещение точки приложения силы вдоль линии ее действия
Если точку приложения силы переместить вдоль линии действия силы, то момент, при таком перемещении, не изменится.
Доказательство
Пусть сила приложена в точке . Через точку проведем прямую, параллельную вектору силы. Эта прямая является линией ее действия. Переместим точку приложения силы в точку , принадлежащую линии действия. Тогда. Вектор проведен через две точки линии действия. Поэтому его направление совпадает или противоположно направлению вектора силы . Тогда , где – параметр; . , если точка смещена относительно в направлении вектора . В противном случае .
Таким образом, вектор, проведенный из в , имеет вид:. Найдем момент силы, приложенной в точке , применяя свойства векторного произведения:. Мы видим, что момент не изменился:.
Свойство доказано.
Абсолютная величина момента силы
Абсолютная величина момента силы относительно некоторой точки равна произведению абсолютного значения силы на плечо этой силы относительно выбранной точки.
Доказательство
Абсолютное значение момента M относительно точки O равно произведению силы F на ее плечо d = |OD|.
Пусть мы имеем силу , приложенную в точке . Рассмотрим момент этой силы относительно некоторой точки . Заметим, что точки , и вектор лежат в одной плоскости. Изобразим ее на рисунке. Через точку , в направлении вектора проводим прямую . Эта прямая называется линией действия силы . Через точку опустим перпендикуляр к линии действия. И пусть является точкой пересечения линии действия и перпендикуляра. Тогда – плечо силы относительно центра . Обозначим его буквой . Воспользуемся , согласно которому точку приложения силы можно перемещать вдоль ее линии действия. Переместим ее в точку . Момент силы:. Поскольку векторы и перпендикулярны, то по свойству векторного произведения, абсолютное значение момента:, где – абсолютное значение силы.
Заметим, что вектор момента перпендикулярен плоскости рисунка. Его направление определяется по правилу правого винта. Если мы будем вращать винт, проходящий через точку перпендикулярно плоскости рисунка, в направлении силы , то он будет перемещаться на нас. Поэтому вектор момента перпендикулярен плоскости рисунка и направлен на нас.
Свойство доказано.
Момент относительно точки от силы, проходящей через эту точку
Момент относительно точки , от силы, линия действия которой проходит через эту точку, равен нулю.
Доказательство
Пусть линия действия силы проходит через точку . Тогда плечо этой силы относительно равно нулю: . Согласно , абсолютное значение момента силы относительно выбранной точки равно нулю:.
Свойство доказано.
Момент суммы сил, приложенных в одной точке
Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:.
Доказательство
Пусть силы приложены в одной точке . Пусть – векторная сумма этих сил. Находим момент относительно некоторой точки от векторной суммы , приложенной в точке . Для этого применяем свойства векторного произведения:.
Свойство доказано.
Момент системы сил, векторная сумма которых равна нулю
Если векторная сумма сил равна нулю:, то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:.
Доказательство
Пусть силы приложены в точках , соответственно. И пусть точки и обозначают два центра, относительно которых мы будем вычислять моменты. Тогда имеют место следующие векторные уравнения:. Используем их при вычислении суммы моментов относительно точки . Здесь мы воспользовались тем, что по условию,.
Свойство доказано.
Момент относительно оси от силы, проходящей через эту ось
Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство
В указано, что момент силы относительно оси – это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси. В качестве такой точки возьмем точку пересечения линии действия силы с осью. Но, согласно , момент относительно этой точки равен нулю. Поэтому равна нулю и его проекция на эту ось.
Свойство доказано.
Момент относительно оси от силы, параллельной этой оси
Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство
Пусть – произвольная точка на оси. Рассмотрим момент силы относительно этой точки. Согласно определению:. Согласно свойству векторного произведения, вектор момента перпендикулярен вектору силы . Поскольку вектор силы параллелен оси, то вектор момента ей перпендикулярен. Поэтому проекция момента относительно точки на ось равна нулю.
Свойство доказано.
Как снять квартиру без залога?
Залог при аренде квартиры в РФ не так распространен, как в Америке и европейских странах. При подборе жилья на рынке недвижимости не более 20 % частных собственников требуют внести предоплату. Риелторы чаще заключают договор с гарантией, чем физические лица, предлагающие снять у них квартиру без посредников, поэтому при поиске жилья без страхового депозита лучше ориентироваться на объявления частных лиц.
Иногда хозяин готов сотрудничать и отказаться от залога, если съемщик убедит его в своей честности и ответственности. Повлиять на решение владельца можно только до заключения договора аренды.
Залог при аренде имущества – гарантия для владельца. Он позволяет частично окупить затраты в случае сдачи жилья недобросовестным клиентам. Для арендаторов гарантийная оплата означает комфортабельные условия проживания.
Юрист о страховом депозите:
Плательщики могут договориться о рассрочке залога, получении скидки или его отмене, если собственник будет уверен в их порядочности. Рекомендуется соглашаться на оплату услуги только при указании страхового депозита в договоре аренды. Это обеспечит выполнение обязательств обеими сторонами в полном объеме.
Бизнес и финансы
БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством
ГДЗ Физика 7 класс. Перышкин отдыхает! Рычаг. Блок. Момент силы
- Подробности
- Просмотров: 140
Назад в «Оглавление»
Давненько пользуемся мы этими учебниками.
Еще наши мамы и папы по ним учились.
Как же осилить домашнее задание, ответить на вопросы и решить задачи в упражнениях?
Уверена, что думающие ученики сначала всё сделают сами, а эти сведения будут помощью «застрявшим в пути».
Ответы на ДЗ по физике помогут вам проверить себя и найти ошибки.
Ответы на ДЗ из упражнений соответствуют всем выпускам учебников этого автора, начиная с 1989 г.
Так как номера упражнений с одинаковыми вопросами в разных выпусках различаются, ответы на вопросы к упражнениям скомпонованы по темам.
На этой странице представлены решения задач по параграфам: Простые механизмы. Рычаг. Равновесие сил на рычаге. Момент силы. Рычаги в технике, быту и природе.
Заодно некоторые узнают, какую тему по физике они сейчас изучают))
Так нет ли здесь нужной вам задачи?
Обязательно найдется!
Решаем вместе?
1. Укажите точку опоры и плечи сил у рычагов, изображенных на рисунках.
а) Тачка с одним колесом.
Схема рычага:
Точка опоры — ось колеса (О).
Плечо силы F1 — от оси колеса до груза на тачке (ОА).
Плечо силы F2 — от оси колеса до рук (ОВ).
б) Рука человека — это тоже рычаг.
Схема рычага:
Точка опоры — локтевой сустав (О).
Плечо силы F1 — длина руки (предплечья) от локтя до кисти, в которую вложен груз (ОА).
Плечо силы F2 — небольшое расстояние (около 3 см) от локтевого сустава до точки прикрепления мышцы плеча на предплечье (ОВ).
в) Ножной тормоз в автомобиле.
Схема рычага:
Рычаг — педаль тормоза.
Точка опоры — ось вращения педали (О).
Плечо силы F1 — кратчайшее расстояние (ОА) от точки опоры до линии приложения силы F1, с которой нога давит на педаль.
Плечо силы F2 — кратчайшее расстояние (ОВ) от точки опоры до линии приложения силы F2 — силы упругости троса, прикрепленного к педали.
д, г) Палка для переноса тяжестей.
Схема рычага:
Здесь точка опоры — плечо человека (О).
Плечо силы F2 — от плеча до места, за которое держат палку (ОВ).
Плечо силы F1 — от плеча до того места, где подвешен груз (ОА).
2. Рассмотрите рисунки переноса груза на палке. При каком расположении груза на палке момент его силы тяжести больше? В каком случае груз легче нести? Почему?
Момент силы тяжести груза больше, когда увеличивается плечо этой силы.
Чтобы легче было нести, надо уменьшить плечо этой силы, т.е.расстояние от плеча до груза.
В этом случае рычаг можно уравновесить меньшей силой рук.3. Пользуясь рисунком гребца в лодке, объясните, почему при гребле мы получаем проигрыш в силе и для чего это нужно.
Весло при гребле на лодке представляет собой рычаг.
Точка опоры — уключина.
С одной стороны к рукоятке весла прикладывается сила человека.
Плечо этой силы небольшая часть весла от уключины до руки.
С другой стороны действующая на весло сила — это сила сопротивления воды.
Плечо этой силы — наиболее длинная часть весла от уключины до конца весла в воде.
Чтобы сделать гребок надо уравновесить этот рычаг,
По правилу равновесия рычага при этом к короткой части весла прикладывается большая сила, а к длинной части весла меньшая сила.
В данном случае наблюдается проигрыш в силе.
Однако при гребке расстояние, которое проходит конец весла много больше расстояния, которое проходит рукоять весла.
Проигрывая в силе, выигрываем в расстоянии, что и является целью передвижения на лодке.
Иногда когда человеку становится трудно грести (он устал), он сдвигает весло в уключине так, чтобы часть весла от руки до уключины стала длиннее. Концы весел в лодке как бы нахлестывают друг на друга, грести становится не очень удобно, зато легче, прикладывается меньшая сила. Но одновременно и расстояние, которое проходит лодка за гребок уменьшается.4. На рисунке 162 изображен разрез предохранительного клапана. Рассчитайте, какой груз надо повесить на рычаг, чтобы пар через клапан не выходил. Давление в котле в 12 раз больше нормального атмосферного давления. Площадь клапана S = 3 см2, вес клапана и вес рычага не учитывать. Плечи сил измерьте по рисунку. Куда нужно переместить груз, если давление пара в котле увеличится? уменьшится? 5. На рисунке изображена схема подъемного крана. Рассчитайте, какой груз можно поднимать при помощи этого крана, если масса противовеса 1000 кг. Сделайте расчет, пользуясь равенством моментов сил.
Назад в «Оглавление»
Кредитное плечо: чем оно выгодно трейдеру
1. Возможность начать торговлю на Форекс с малых сумм
Мы уже выяснили, что торговать целым лотом на валютном рынке очень дорого, поэтому не каждый трейдер может себе это позволить. Условия маржинальной торговли позволяют снизить необходимую сумму капитала для начинающих трейдеров. Например, если у вас есть начальный депозит в $1000, используя кредитное плечо 1:100, вы фактически можете заключать сделки на сумму $100 000, а это уже, согласитесь, куда большие возможности.
2. Пропорциональное увеличение прибыли
Кредитное плечо позволяет увеличить размер торгового лота. Например, если без использования маржинальных условий ваших денег на счете хватит на открытие сделки 0,01 частью лота, то при плече 1:100 вы можете открыть позицию размером в 1 лот. А это значит, что и прибыль в сделке будет в 100 раз больше. Таким образом, леверидж-торговля хороша для «разгона» небольших депозитов.
3. Доступ к диверсификации
Чем больше сумма на вашем торговом счете, тем больше сделок вы можете открыть. А следовательно, вы можете диверсифицировать торговый портфель и увеличить вероятность прибыльных сделок.
4. Выгодные кредитные условия
Пользуясь кредитным плечом, вы фактически берете кредит у брокера. За пользование этими деньгами вы платите комиссию — спред. Также по открытым сделкам, которые переносятся через ночь, начисляется своп.
Если бы вы взяли такую же сумму в банке, это было бы гораздо дороже. К тому же все заемные средства необходимо было бы вернуть, заплатив процент, даже если бы вы ими не пользовались.
Лабораторная работа №7 Сила мышц и силовая выносливость
Цель
работы:
определить силу мышц кисти и силовую
выносливость.
Объект
исследования:
человек.
Материалы
и оборудование: кистевой
динамометр ДК-100, секундомер.
Определение
силы мышц кисти
Сила мышцы
определяется максимальным грузом,
который она способна поднять.
Сила
скелетной мышцы зависит от ряда факторов:
исходной длины, при которой мышца
развивает максимальное сокращение
(максимальная сила развивается в том
случае, если длина саркомера составляет
2,2—2,5 мкм); числа двигательных единиц
(ДЕ), возбуждаемых в
данный момент времени; синхронности
работы ДЕ; частоты приходящих
к ним по аксонам потенциалов действия.
Ход
работы:
Измерение
силы мышц кисти производят с помощью
кистевого динамометра. Сила сжатия его
стальной пружины регистрируется
стрелкой. Испытуемый берет кистевой
динамометр в правую руку и отводит ее
в сторону так, чтобы между конечностью
и туловищем был прямой угол. Вторую руку
опускает вдоль туловища, затем
сжимает динамометр пальцами правой
кисти с максимальной силой
несколько раз, делая интервалы в 1 — 2 мин
и каждый раз фиксируя
положение стрелки динамометра. Наибольшее
ее отклонение является показателем
максимальной силы мышц кисти. Затем
испытуемый
проводит такое же измерение с левой
рукой.
Относительную
силу мышц кистей правой и левой рук
определить по
формуле
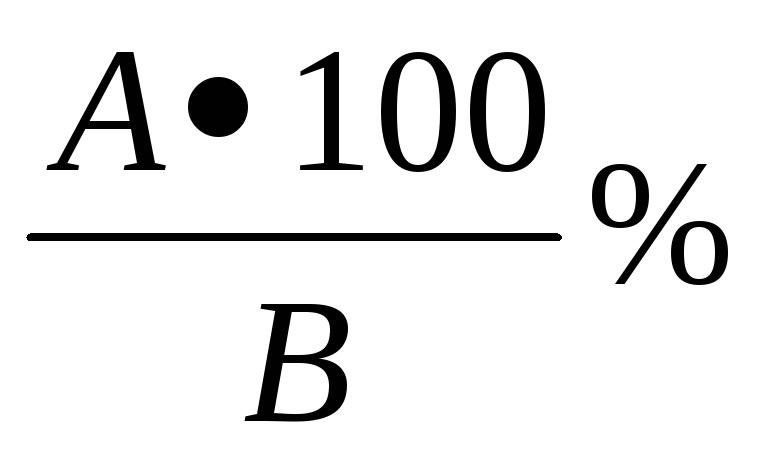
где
А
— сила
мышц правой или левой руки; В
— масса
тела (кг).
Сила
сжатия пружины динамометра эквивалентна
массе груза, следовательно, значения
по динамометру выражаются в килограммах.
Среднестатистические показатели
относительной величины силы кисти
для мужчин составляют 60 — 70 %,
для
женщин — 45-50 %.
Определение
силовой выносливости
Ход
работы:
Для
определения силовой выносливости мышц
верхней
конечности экспериментатор уменьшает
силу сжатия ручного динамометра
так, чтобы она составляла 30 % от
максимальной. Далее по
команде испытуемый пытается удержать
такое усилие как можно дольше.
Экспериментатор по секундомеру определяет
время. Через несколько
минут опыт повторяют, при этом сила
сжатия уменьшается до
значения 50 % от максимальной.
Задание.
Определить среднее значение силовой
выносливости в группе,
результаты записать в тетрадь. Дать
рекомендации по повышению
силы кистей рук и силовой выносливости.
Ответить на вопросы:
что такое саркомер, ДЕ? От чего зависит
синхронность работы мышечных волокон
в двигательной единице? Какова возбудимость
мышечных
волокон, входящих в одну и ту же ДЕ?
Используем векторы для изучения вращательного движения
В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.
Определяем направление угловой скорости
Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!
Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость ( omega ), оказывается, направлена вдоль оси вращающегося колеса (рис. 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.
Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.
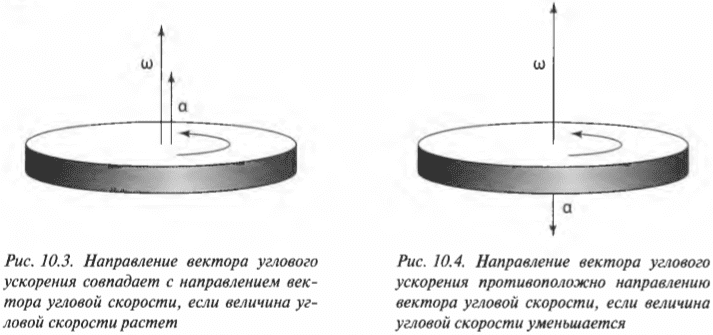
Определяем направление углового ускорения
Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:
где ( alpha ) — угловое ускорение, ( Deltaomega ) — изменение угловой скорости, ( Delta t )— время изменения угловой скорости.
В векторной форме оно имеет следующий вид:
где ( mathbf{alpha} ) — вектор углового ускорения, а ( Deltamathbf{omega} ) — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.
Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.
Что такое рычаг силы?
Рычаг силы играет важную роль при определении величины момента силы. Чтобы понять, о чем идет речь, рассмотрим следующий рисунок.
Здесь показан некоторый стержень длиною L, который закреплен в точке вращения одним из своих концов. На другой конец действует сила F, направленная под острым углом φ. Согласно определению момента силы, можно записать:
Угол (180o-φ) появился потому, что вектор L¯ направлен от закрепленного конца к свободному. Учитывая периодичность тригонометрической функции синуса, можно переписать это равенство в таком виде:
Теперь обратим внимание на прямоугольный треугольник, построенный на сторонах L, d и F. По определению функции синуса, произведение гипотенузы L на синус угла φ дает значение катета d
Тогда приходим к равенству:
Линейная величина d называется рычагом силы. Он равен расстоянию от вектора силы F¯ до оси вращения. Как видно из формулы, понятием рычага силы удобно пользоваться при вычислении момента M. Полученная формула говорит о том, что вращающий момент максимальный для некоторой силы F будет возникать только тогда, когда длина радиус-вектора r¯ (L¯ на рисунке выше) будет равна рычагу силы, то есть r¯ и F¯ будут взаимно перпендикулярны.
Как принцип рычага реализован в нашем теле
Рычаг — это тело, которое может вращаться вокруг неподвижной опоры. Он помогает поднять больше веса с меньшими усилиями. У него есть точка опоры и ось вращения. Есть сила, которую прикладывают к его концу, и плечо силы — кратчайшее расстояние от оси вращения до точки приложения силы.
Крутящий момент = сила × плечо силы
И чем длиннее плечо, тем больше крутящий момент.
Принцип рычага
Все наши суставы работают по принципу рычага. Мышцы с помощью сухожилий крепятся к костям, сокращаются и тянут их, совершая движение. Например, две головки бицепса, двуглавой мышцы плеча, крепятся к лучевой кости. Когда вы сгибаете руку, бицепс сокращается (сила) и создаёт крутящий момент в локтевом суставе (ось вращения). Чем толще ваша двуглавая мышца, тем сильнее увеличивается крутящий момент. И это понятно: накачанный атлет поднимет больше, чем худенькая девочка.
Принцип рычага в работе бицепса плеча
В то же время имеет значение и плечо силы — расстояние от точки вращения до места приложения силы. Поэтому чем больше расстояние от сустава до точки прикрепления сухожилия, тем сильнее человек. Однако это физиологические особенности строения, которые невозможно изменить. Да и отличия между людьми в этом плане не такие уж большие.
Другое дело — плечо до точки приложения противодействующей силы, например, гири, штанги или веса своего тела. Возьмём тот же пример со сгибанием руки в локте, только добавим гантель для наглядности.
Плечо силы от гантели до локтя в разных фазах сгибания на бицепс
Когда вы сгибаете руку, ось вращения находится в локтевом суставе (зелёная точка). Точка приложения силы — это гантель, которая тянет руку вниз под действием гравитации (красная точка). А плечо силы — перпендикуляр от локтя до оси, по которой проходит гантель (зелёная линия).
Когда вы опускаете руку, уменьшается плечо силы, а вместе с ним и нагрузка на бицепс. Плечо силы максимально, когда предплечье параллельно полу, а значит, в этой точке наиболее сильна и нагрузка на мышцы.
Сила трения
Сила трения – это сила, возникающая при движении тел или при попытке сдвинуть их с места вследствие неровностей поверхностей соприкасающихся тел.
Сила трения действует на поверхности тел и затрудняет их перемещение относительно друг друга.
Сила трения всегда направлена противоположно относительному перемещению тела, т. е. против направления вектора скорости.
Виды трения
Внешнее трение (сухое) – это трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении.
Сила трения покоя – это сила, которая возникает между соприкасающимися и покоящимися относительно друг друга поверхностями, а также при попытке сдвинуть тело с места.
Сила трения покоя саморегулирующаяся, т. е. в зависимости от внешних воздействий она может меняться от 0 до максимального значения.
где \( \mu \) – коэффициент трения, \( N \) – сила реакции опоры.
Если в условии задачи не говорится, что сила трения покоя максимальна, то ее надо находить через другие силы по второму закону Ньютона.
Cила трения скольжения – это сила, которая возникает между соприкасающимися и движущимися относительно друг друга телами.
Сила трения качения – это сила, которая возникает между соприкасающимися и катящимися относительно друг друга телами.
Внутреннее трение (жидкое или вязкое) – между слоями жидкости или газа, скорости которых меняются от одного слоя к другому.
Если движение происходит по гладкой поверхности, то сила трения равна нулю.
Способы уменьшения трения:
- выравнивание соприкасающихся поверхностей;
- смазка;
- установка шариковых и роликовых подшипников.
Важно!
Сила трения не зависит от площади соприкосновения трущихся поверхностей. Она зависит от относительной скорости тел
В этом ее главное отличие от сил тяготения и упругости, зависящих только от координат.
Важно!
Если тело удерживается на горизонтальном вращающемся диске силой трения, то
Заблуждения о кредитном плече
Существует масса всевозможных жалоб и мелких заблуждений, которые я часто встречаю в отзывах о брокерах или в иных сообществах, но всё это обычно перекладывание ответственности за слитый депозит на других. Вот пару примеров:
Forex-брокеры специально делают огромные плечи, чтобы мы сливали счета. По большей части данное заявление неверно, вы сами можете регулировать используемый кредит через личный кабинет, либо в терминале путем подбора лота. Для «полного нуля» в трейдинге, конечно, плечо станет губительным. Собственно говоря, наивные и недальновидные люди во всех сферах деятельности терпят крах (берут непосильные кредиты на дорогой смартфон, автомобиль и т.д.), пока жизнь их не научит.
Чтобы не слить счет, нужно торговать с рычагом 1:1. Не факт. К примеру, скальпингом внутри дня 1 к 1 вы мало, что заработаете, для этого и создан большой леверидж. Чем дольше планируете держать позицию, тем меньшее плечо (лот) понадобится. Поэтому, рычаг — это оружие, которое в руках обезьяны, конечно, может сотворить беду, а разумного человека сделает только могущественнее.
Кроме того, многие новички думают, что деньги под плечо трейдеру даются брокером безвозмездно, но это не совсем так. Есть такое явление, как swap (что это?) при переносе позиции на следующий день. Он как раз и списывает с вас те самые годовые проценты за пользование заёмными средствами, но только за одни сутки из 365. Его размер зависит от ставок рефинансирования. Чем дольше пользуетесь деньгами, тем больше и заплатите по итогу через своп. Внутри дня — по факту получаете кредит без процентов.
Переходим от прямолинейного движения к вращательному
Для такого перехода нужно изменить уравнения, которые использовались ранее для описания прямолинейного движения. В главе 7 уже упоминались некоторые эквиваленты (или аналоги) из мира прямолинейного и вращательного движения.
Вот как выглядят основные формулы прямолинейного движения, которые подробно описываются в главе 3:
- ( v=Delta{s}/Delta{t} ), где ( v ) — это скорость, ( Delta{s} ) — перемещение, a ( Delta{t} ) — время перемещения;
- ( a=Delta{v}/Delta{t} ), где ( a ) — это ускорение, ( Delta{v} ) — изменение скорости, a ( Delta{t} ) — время изменения скорости;
- ( Delta{s}=v_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 ), где ( v_0 ) — это начальная скорость, ( t_0 ) — это начальный момент времени, a ( t_1 ) — это конечный момент времени;
- ( v^2_1-v^2_0=2aDelta{s} ), где ( v_1 ) — это конечная скорость.
По аналогии можно легко вывести основные формулы вращательного движения:
- ( omega=Delta{theta}/Delta{t} ), где ( omega ) — угловая скорость, ( Delta{theta} ) — угол поворота, ( Delta{t} ) — время поворота на угол ( Delta{theta} );
- ( alpha=Delta{omega}/Delta{t} ), где ( alpha ) — угловое ускорение, ( Delta{omega} ) — изменение угловой скорости, ( Delta{t} ) — время изменения угловой скорости;
- ( theta=omega_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 ), где ( omega_0 ) — это начальная скорость;
- ( omega^2_1-w^2_0=2as ), где ( omega_1 ) — это конечная скорость.
Равновесие рычага
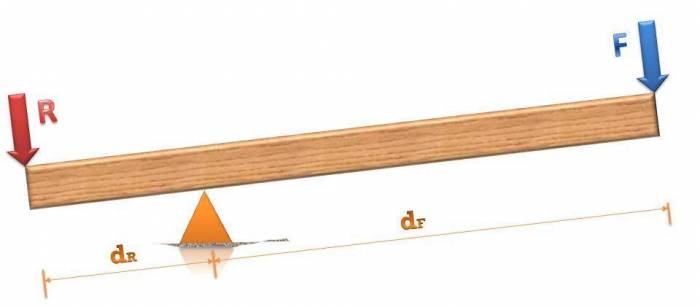
На рисунке выше показан типичный рычаг и отмечены силы, которые на него действуют. Далее в статье будет сказано, что это — рычаг первого рода. Здесь буквами F и R отмечены внешняя сила и некоторый вес груза соответственно. Также видно, что опора смещена относительно центра, поэтому длины плеч dF и dR не равны друг другу.
В статике показано, чтобы рычаг не двигался как целый механизм, должна нулю равняться сумма всех сил, которые на него действуют. Мы отметили только две из них. На самом деле существует еще и третья, которая этим двум противоположна и равна их сумме — это реакция опоры.
Чтобы рычаг не совершал вращательные движения, необходимо, чтобы сумма всех моментов сил была равна нулю. Плечо силы реакции опоры равно нулю, поэтому момента она не создает. Остается записать моменты сил F и R:
Записанное условие равновесия рычага в виде формулы, также приводится:
Это равенство означает, что для того, чтобы рычаг не совершал вращение, внешняя сила должна быть во столько раз больше (меньше) веса поднимаемого груза, во сколько раз плечо этой силы меньше (больше) плеча, на которое действует вес груза.
Приведенная формулировка означает, что во сколько раз мы выигрываем в пути с помощью рассматриваемого механизма, во столько же раз проигрываем в силе.
 Плечом силы называется
Плечом силы называется Метод определения силы мышц кисти называется кистевая динамометрия
Метод определения силы мышц кисти называется кистевая динамометрия Что такое кредитное плечо?
Что такое кредитное плечо?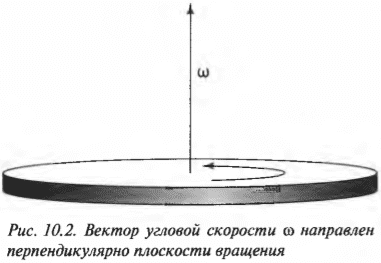
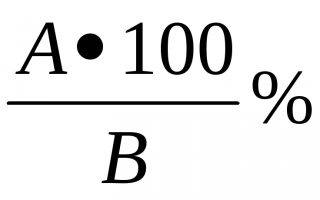

 Костяшки пальцев потемнели
Костяшки пальцев потемнели Упражнения с гантелями для спины
Упражнения с гантелями для спины Бросок через плечо: техника выполнения
Бросок через плечо: техника выполнения Как работать с точкой здоровья юн цюань
Как работать с точкой здоровья юн цюань